Diseño de un personaje con tangencias

A pesar de que este trabajo nos ha llevado muchísimo tiempo (más del que me hubiera gustado), el resultado ha merecido la pena. 
Aunque aquí no se aprecia, nos hemos detenido mucho en cada una de las FASES DEL PROYECTO, valorando así la importancia de todas y cada una de ellas. 
Los BOCETOS PREVIOS han tenido a nivel de calificación la misma importancia que el RESULTADO FINAL, o tal vez dicho resultado es satisfactorio por no ser fruto de la casualidad sino del trabajo que hay tras él.      
La mayoría de los autores de estos estupendos trabajos  tienen otros de la misma calidad que también aparecen en alguna otra entrada. 



Diseño de un personaje con tangencias

View more presentations from ESTER ALONSO

TANGENCIAS Y ENLACES (CURVAS TÉCNICAS)

Antes de realizar un ejercicio más artístico tendremos que realizar una serie de ejercicios de tangencias entre circunferencias.

Dos circunferencias son tangentes cuando tienen un punto en común. Dicho punto se denomina punto de Tangencia (T).

CONDICIÓN DE TANGENCIA ENTRE CIRCUNFERENCIAS.
Debemos saber que si dos circunferencias son tangentes, el punto de tangencia  estará necesariamente en la línea que une los centros.

Vamos a realizar cinco ejercicios en esta lámina.
Os los dejo en formato Mongge, para que podáis seguir paso a paso la construcción.






Lógicamente, si tomamos como centro primer centro otro punto de la mediatriz del primer segmento, se modifica también la forma de la envolvente.
No olvidéis que los centros deben quedar siempre alineados con los puntos de tangencia.

GEOMETRÍA Y TEXTURAS EN LA NATURALEZA

Nuestro próximo trabajo se centra de nuevo en el mundo de la GEOMETRÍA y los POLÍGONOS REGULARES.

Esta vez os proponemos "mirar" a vuestro alrededor, para buscar en las formas orgánicas de la naturaleza la FORMA MATEMÁTICA subyacente.

Podéis encontrar la SIMETRÍA RADIAL (Composición equilibrada en torno a uno o más ejes centrales)  en la disposición de los pétalos de las flores, en las estrellas de mar,  en los copos de nieve...

Pero...¿qué tienen que ver las matemáticas con la naturaleza, y con nuestra concepción de la belleza...Lo comprenderás tras ver este vídeo. (No olvides el número de oro y la sucesión de Fibonacci)

Navegando he podido encontrar este maravilloso video de Cristóbal Vila que nos da una visión más poética de lo que se nos explica en el video anterior.

Geometría y texturas en la naturaleza from ESTER ALONSO

DIVISIÓN REGULAR DE LA CIRCUNFERENCIA Y SIMETRÍA RADIAL (POLÍGONOS)

Antes de realizar el próximo trabajo debemos recordar conceptos que vísteis en 1º de ESO.
Si dividimos la circunferencia de forma regular obtendremos los polígonos (regulares también).
Las construcciones del triángulo equilátero, el hexágono y el dodecágono están relacionadas entre sí, cosa que ocurre también con el cuadrado y el octógono.
             Si los vértices de los polígonos se unen de forma no consecutiva podemos obtener los llamados polígonos estrellados.
No todos los polígonos tienen su correspondiente estrellado.
El trazado deberá hacerse de forma que "nos saltemos" un número determinado de vértices. A ese número lo vamos a llamar paso. En un polígono de paso dos como es el caso del pentágono, nos saltaríamos un vértice para unir con el siguiente. Para que el estrellado sea tal deberemos terminarlo en el vértice con el que comenzamos su trazado y todo ello sin necesidad de levantar el lápiz del papel.
El número de vértices que nos saltamos no puede ser divisor del número de vértices, ya que de ser así llegaríamos al primer vértice sin pasar por todos los demás. El hexágono, por ejemplo, no tiene estrellado posible ya que si nos saltamos dos vértices lo que obtendríamos en realidad es dos triángulos equiláteros girados 180º.

Para dibujar el pentágono regular inscrito en una circunferencia necesitaréis seguir estos pasos:

Nuestro próximo trabajo se centra de nuevo en el mundo de la GEOMETRÍA y los POLÍGONOS REGULARES.

Esta vez os proponemos "mirar" a vuestro alrededor, para buscar en las formas orgánicas de la naturaleza la FORMA MATEMÁTICA subyacente.

Podéis encontrar la SIMETRÍA RADIAL (Composición equilibrada en torno a uno o más ejes centrales)  en la disposición de los pétalos de las flores, en las estrellas de mar,  en los copos de nieve...

SIMETRÍA RADIAL: MANDALAS

Mandalas 3º from ESTER ALONSO

SIMETRÍA RADIAL

Vamos a realizar un trabajo sobre la Simetría radial, pero antes utilizaremos en el aula de informática varios applets de GeoGebra.

Os dejo enlazada la construcción del vídeo que tiene la ventaja de que el color se genera automáticamente y lo hace de forma dinámica, es decir, variará en función de donde esté situado  cursor, que es el que determina el dibujo resultante. Cada uno de los trazos que hagamos con este punto (rojo) será simétrico respecto a un radio y se verá multiplicado por el número de divisiones  que elijamos para la circunferencia (entre 3 y 12).

Enlazada a la imagen os dejo un link a otra construcción similar, pero que se diferencia de la anterior en que en este caso sois vosotros los que elegís los colores.
Os dejo un vídeo para que os resulte más fácil utilizar cualquiera de las dos construcciones.
Cuando una figura presenta una simetría radial puede ser girada de manera que su forma vuelva a coincidir consigo misma tras el giro. En el caso del cristal de nieve, la simetría que presenta es de orden seis, ya que su forma coincide este número de veces en una vuelta.
En el siguiente applet puedes apreciarlo. Prueba a dibujar con el cursor una de las ramas de dicho cristal y comprobarás que la forma se completa con bastante precisión.

PERSPECTIVA CÓNICA FRONTAL

Vamos a realizar dos trabajos utilizando este tipo de perspectiva. En el primero de ellos dibujaremos dos prismas, y en el segundo y partiendo de unas medidas determinadas dibujaréis una habitación. En ella situaréis una serie de muebles cuyas medidas os daré.
Mientras os vais animando a entregarme los trabajos os dejo una pequeña muestra de ellos con sus correspondientes bocetos.

P CÓNICA

Publish at Calameo or read more publications.

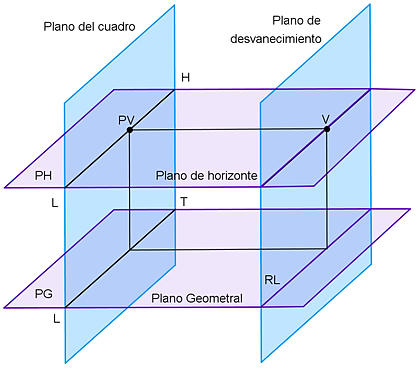
En la imagen podéis ver los distintos elementos que intervienen en este tipo de perspectiva que es, dentro de los Sistemas de Representación aquél que más se acerca a la visión humana (monocular).
Haced clic sobre ella para ampliarla y verla con más detalle.

En la imagen os enlazo una construcción interactiva de GeoGebra para que entendáis mejor cómo afecta el punto de vista, la altura de la Línea de Horizonte, así como las dimensiones de la habitación en la visión que tenemos de ésta.

Si hacéis clic nuevamente sobre la imagen podréis acceder a otra construcción interactiva.

Es interesante que modifiquéis las dimensiones de los planos y tratéis de situarlos según una serie de premisas.

Por ejemplo:

Sitúa un poster de 1 m de altura y 1/2 de anchura sobre la pared de la izquierda de forma que quede situado a 1 m de profundidad y a una altura de metro y medio...

Coloca en el suelo una alfombra de 2 m por 3m ...,etc.

Os será de todas formas mucho más fácil hacerlo sobre la construcción que tenéis debajo.

https://www.geogebra.org/m/bBXhtXHZ

Una vez que hayáis entendido como se deben tomar medidas en este tipo de perspectiva diseñaréis vuestra propia habitación.
Las medidas van a ser las mismas para todos.
La planta de la habitación es cuadrada (4x4 m), con lo que tendremos una superficie de 16 m2.
El boceto lo haréis sobre la fotocopia que os daré y lo trabajaréis después con color en una lámina DIN A4.

En esta otra imagen tenéis el enlace al applet de GeoGebra que ya os enseñé al hablaros de los Sistemas de Representación y que utilizaré para explicaros el primero de los trabajos que vamos a realizar.

 Si pulsáis sobre la imagen accederéis a otra construcción en la que podréis situar el punto de fuga así como las líneas que se dirigen hacia él sobre distintos cuadros del pintor hiperrealista Antonio López.