PAISAJE ISOMÉTRICO

Os dejo una preciosa perspectiva isométrica de un paisaje urbano realizada el año pasado por vuestro compañero Miguel Angel (3º C).

Para hacer el hexágono inscrito en la circunferencia sigue estas instrucciones.http://www.mongge.com/educacion/dibujo-tecnico/ejercicios/1487/

NIVELES 1 Y 2 (vistas, axonometría y Aumentaty)

Os dejo aquí el vídeo con las piezas que hemos hecho en clase, en Realidad Aumentada para aquellos que aún no las hayan "visto".
En la Galería 3D Warehouse de SketchUp podéis ver algunas más.

REPRESENTACIÓN DE PIEZAS EN 3D

Esta pieza está realizada con el programa de geometría dinámica GeoGebra en su versión 5, que incluye una vista 3D.
Sitúate sobre la pieza representada en la vista 3D y pulsando el botón derecho del ratón y sin soltarlo rótala. Puedes girarla para comprobar la corrección de las vistas diédricas situadas a la derecha.
En este caso se pedía la representación del perfil derecho a partir de las vistas del alzado y la planta.


Vamos a intentar construir las piezas que cada uno de vosotros habéis dibujado en papel, en 3D con el programa gratuito Trimble SketchUp. Os dejo en este enlace el cubo de 4x4x4 unidades con las guías preparadas para que ni siquiera tengáis que medir. Debéis descargarlo y trabajar la pieza con el programa.
Para muchos este programa será nuevo, pero podréis comprobar que es muy fácil aprender a manejarlo con tan solo unas pequeñas indicaciones.
Os dejo aquí un vídeo para que veáis como podéis usarlo.
Aquí tenéis un ejemplo de lo que podría ser una de vuestras piezas.
Y lo que debéis hacer es construirla con SketchUp.
Para que sea más sencillo entender posteriormente las vistas de las piezas, deberéis colorear el alzado y la vista posterior en amarillo, los perfiles en magenta y la planta en azul. Las rampas se harán del color que resulte de la mezcla de las dos vistas desde la que se ve. En este caso, por tratarse de la planta y el alzado el color a utilizar sería el verde.

Si quieres ver la pieza en REALIDAD AUMENTADA con Aumentaty, deberás descargarte el visor e imprimir el marcador al que va asociado la pieza. Aquí tenéis el enlace.

Os dejo un vídeo en el que podéis ver como funciona Aumentaty y lo estupendo que puede ser para la enseñanza de la axonometría y las vistas diédricas.
Aquellos que el año que viene tengáis informática como optativa, aprenderéis a utilizar el programa durante el curso. La versión que vamos a utilizar es la 8. Os la dejo enlazada por si quisiérais descargarla y utilizarla en casa.
Por si a alguno le interesa ir más allá de lo básico, aquí tenéis un completo manual.

SISTEMAS DE REPRESENTACIÓN

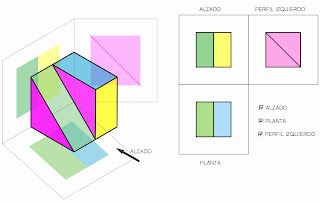Cuando dibujamos, representamos objetos de tres dimensiones en un papel que tan solo dispone de dos. Esto nos hace recurrir a diferentes sistemas de proyección de dicho objeto sobre el soporte. En función de las necesidades utilizaremos uno u otro. No es lo mismo realizar un dibujo inequívoco para fabricar un objeto, que proyectar otro, lo más parecido posible a la representación que realiza un arquitecto para que su cliente pueda visualizar cómo va a quedar su futura vivienda. En el primero de los casos realizaremos los dibujos en el Sistema Diédrico (las temidas vistas), y en el otro trabajaremos en Perspectiva Cónica.

En esta presentación podéis ver una comparativa entre los distintos Sistemas de Representación, así como sus fundamentos.

Os enlazo en las imágenes además unos applets interactivos de GeoGebra, (un programa de Geometría Dinámica que suele usarse para la enseñanza de las matemáticas) para que podáis apreciar las diferencias entre unos y otros.

ISOMETRÍA Y VISTAS DIÉDRICAS

Si hacéis clic sobre la imagen podréis acceder a un applet de GeoGebra con el que podréis ver la diferencia que existe entre elegir una u otra vista como alzado, así como en que posición se representan en el Sistema Europeo los distintos perfiles.
 Os recomiendo que veáis el vídeo para entender cómo se abaten los planos de proyección y por qué es tan importante que exista correspondencia entre las alturas del alzado y el perfil, así como entre las anchuras del alzado y de la planta, así como de las profundidades de la planta y del perfil.
Aquí tenéis el enlace a la página de educacionplastica.net con el que hacer prácticas con distintos niveles de complejidad.
Os dejo una pequeña explicación sobre el uso de esta herramienta en formato vídeo.

COMPOSICIÓN MODULAR TRIANGULAR

Para realizar una composición modular que cubra un plano vamos a utilizar la forma del triángulo equilátero, que junto con el cuadrado y el hexágono, tiene la capacidad de dividir o teselar el plano cubriéndolo por completo.
Generaremos un módulo triangular utilizando para ello dos tintas (colores), que sumadas al blanco del soporte (lámina Basik), nos dará un total de tres colores.
Giraremos y/trasladaremos luego ese polígono regular para comprobar como el dibujo que se genera es diferente si giramos el módulo 60º respecto a un centro, o si lo giramos 180º.
Coloca los módulos triangulares sobre la red para comprobarlo.
Tienes además los dos ejemplos de los que hemos hablado antes asociados a las correspondientes casillas.


Os dejo como ejemplo el trabajo que realizaron compañeros vuestros del mismo nivel hace algunos años.

Redes modulares y división regular del plano from ESTER ALONSO

La composición modular puede realizarse también utilizando como base un cuadrado.
Si además utilizamos traslaciones podemos llegar a realizar formas como éstas.
Puedes manipular la construcción para modificar su forma.

SIMETRÍA AXIAL Y CUATRICROMÍA

Simetría axial y cuatricromía from ESTER ALONSO

MOVIMIENTOS EN EL PLANO: SIMETRÍA AXIAL Y COLOR

Miguel Angel A. (3º ESO C)

Los próximos trabajos que haremos tratan sobre los llamados movimientos en el plano, conocidos también como transformaciones geométricas.
Para que comprendáis mejor este concepto vamos a ver esta otra entrada del blog de 1º de bachillerato.
El primero de los trabajos que vamos a realizar tiene que ver con la simetría axial y con la cuatricromía.
Vais a necesitar una imagen de buena calidad extraída de una revista (preferiblemente de papel cuché). Esa fotografía debe tener un eje de simetría y ser completamente frontal.
Si sois diestros os va a resultar más cómodo quedaros con la parte izquierda de la imagen,para dibujar la derecha sin taparos el modelo.
Si sois zurdos os resultará más fácil localizar a un compañero que os pueda ceder la parte derecha de una imagen.
Para aquellos que  decís no saber dibujar podéis intentar realizar el trabajo dando la vuelta a la imagen, de esta forma evitaréis reconocer las formas, y os tendréis que guiar tan solo por las relaciones angulares y de posición de los distintos elementos, de esta forma dibujaremos con el hemisferio derecho del cerebro.
El trabajo consiste en dibujar de la forma más simétrica posible la otra parte de la imagen.
Tened en cuenta que es muy importante que peguéis la fotografía sobre un papel poroso (Papel Basik por ejemplo), ya que si la superficie es satinada no conseguiréis saturar los colores (os quedarán muy claros).
Lo más complicado de este trabajo es conseguir igualar el color de la fotografía. Para conseguir algunos tonos necesitaréis incluir rotuladores.
Fijáos en el precioso trabajo que hizo el año pasado vuestro compañero Miguel Angel...(si hacéis clic sobre la imagen podréis verla ampliada).




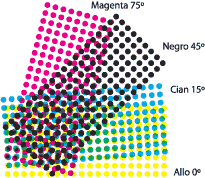
Las revistas al igual que los libros siguen un complejo proceso hasta llegar a nuestras manos.
En la imprenta los cuatro colores (de ahí el nombre de cuatricromía) se van a aplicar por separado. Esos cuatro colores son el Magenta, el cian, el amarillo y el negro (colores pigmento).

Por si queréis saber algo más sobre éste proceso, os dejo este interesante vídeo.